I am looking into how to implement a function to sort the order of leaves in the dendrogram.  If you can recommend someone or books for this task, please let me know.  It should be simple but the data structure of hierarchical clustering output in R is not so straightforward. I do this data processing to recreate tree data structure in Java, and there are ways to call Java from R but this creates Java dependency, and it would be nice if this can be processed in native R.

Here is a code to generate a simulation dataset:

set.seed(1234); par(mar=c(0,0,0,0))
x <- rnorm(12, mean=rep(1:2, each=5), sd=0.3)
y <- rnorm(12, mean=rep(c(1,2,1), each=4), sd=0.3)
dataFrame &lt;- data.frame(x=x, y=y, row.names=c(1:12))

##calculate distance and cluster
distxy <- dist(dataFrame)
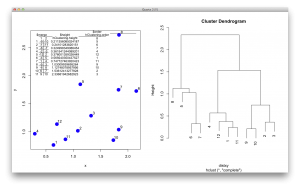
hClustering <- hclust(distxy)

There are 4 key values in the hclust output object, named “hClustering” in the code.

• merge
  • an n-1 by 2 matrix. Row i of merge describes the merging of clusters at step i of the clustering. If an element j in the row is negative, then observation -j was merged at this stage. If j is positive then the merge was with the cluster formed at the (earlier) stage j of the algorithm. Thus negative entries in merge indicate agglomerations of singletons, and positive entries indicate agglomerations of non-singletons.
• height
  • a set of n-1 real values (non-decreasing for ultrametric trees). The clustering height: that is, the value of the criterion associated with the clustering method for the particular agglomeration.
• order
  • a vector giving the permutation of the original observations suitable for plotting, in the sense that a cluster plot using this ordering and matrix merge will not have crossings of the branches.
• labels
  • labels for each of the objects being clustered.

These description is not easy to understand, so I generated a figure to make sense of this output. The picture below shows the data points in a scatter plot and a dendrogram. $merge indicates the order of how leaves/observations are merged.  For example, observation 9 and 10 are merged first and they have the smallest distance, as seen in $height. It repeats this way, and you see -12 and 2 in the 5th row of $merge.  In this case, the number 2 refers to the cluster formed at the 2nd row in the table. (I know… this is a bit confusing… but it is an efficient way to store the hierarchical information. $order is the order of observations as shown in a dendrogram, from the left to the right.

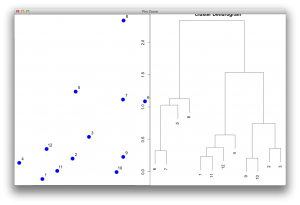
I guess the most important parameter is the $order. The function for reordering should manipulate the $order, then the dendrogram would be drawn according to the sorted order. Here I directly manipulated the order in the object and redrawn the dendrogram without changing any other parameters.

The goal is to automate this process in R and here is  how I implemented in Java. First, I turn the data into a binary tree data structure, using 2 classes and 1 interface. MergedNode is where 2 observations or clusters are merged, and Node class is for each observation. Going though the $merge data, I merge objects until I end up with 1 trunk/root.

class MergedNode implements DendrogramNode{
	DendrogramNode left;
	DendrogramNode right;
	float distance;
        ...
}
class Node implements DendrogramNode{
	IndexObject index;

}
public interface DendrogramNode{
	public DendrogramNode getLeft();
	public DendrogramNode getRight();
	public int getCount();
	public ArrayList<DendrogramNode> getNodes();
	public ArrayList<IndexObject> getIndexObjects();
	public boolean isMergedNode();

}

Once I have the data structure, I sort the left and right DendrogramNode recursively from the root by calculating the average distance. The following function first checks if left or/and right are a observation or a cluster.  If it both are observations, there is not need to swap.  If the left is  a cluster, I don’t swap but look further into the cluster recursively. If the right is a cluster, I swap left and right, because a cluster would have merged nodes within that are smaller distance. If both ends are clusters, then I calculate the average distance of the cluster and the cluster with a smaller value will be placed on the left.

void sortByAverageDistance(MergedNode mn){
	if(mn.leftIsSampleNode && mn.rightIsSampleNode){
		//no need of ordering
	}else if(!mn.leftIsSampleNode && mn.rightIsSampleNode){
		MergedNode left= (MergedNode)mn.left;
		//order within left
		sortByAverageDistance(left);
	}else if(mn.leftIsSampleNode && !mn.rightIsSampleNode){
		MergedNode right_mn = (MergedNode)mn.right;
		//order within right
		sortByAverageDistance(right_mn);
		//need to swap left and right
		rotateMergedNode(mn);
	}else if(!mn.leftIsSampleNode && !mn.rightIsSampleNode){
		MergedNode left_mn = (MergedNode)mn.left;
		MergedNode right_mn = (MergedNode)mn.right;
		if(left_mn.getAverageDistance() > right_mn.getAverageDistance()){
			rotateMergedNode(mn);
		}
		//look further down
		sortByAverageDistance(left_mn);
		sortByAverageDistance(right_mn);
	}
}

The average value of a cluster is calculated by summing distances for all the clusters within, then dividing by n-1, where n is the total number of observations in the cluster. Calculation of the distance sum is recursive as well. 

public float getAverageDistance() {
  float sum = getDistanceSum();
  ArrayList<IndexObject> array = getIndexObjects();
  float average = sum / (float) (array.size()-1);
  return average;
}

public float getDistanceSum(){
  float result = distance;
  if(leftIsSampleNode && rightIsSampleNode){
    result = distance;
  }else if(!leftIsSampleNode && rightIsSampleNode){
    MergedNode left_mn = (MergedNode) left;
    result += left_mn.getDistanceSum();
  }else if(leftIsSampleNode && !rightIsSampleNode){
    MergedNode right_mn = (MergedNode) right;
    result += right_mn.getDistanceSum();
  }else{
    MergedNode left_mn = (MergedNode) left;
    result += left_mn.getDistanceSum();
    MergedNode right_mn = (MergedNode) right;
    result += right_mn.getDistanceSum();
  }
  return result;
}