Bi-Persistence Clustering on the Diabetes Dataset

In 1979, Reaven, Miller & Alto analysed the difference between chemical and overt diabetes in 145 non-obese adults. Previously, they had found a “horseshoe” relation between plasma glucose and insulin response levels, confirmed by later studies. However, the interpretation of this relationship remained unclear. It could be interpreted as the natural progression of diabetes or as different underlying causes for the disease. In their 1979 work, they attempted to quantify the relationship to gain insight into the pattern.

This notebook demonstrates how BPSCAN can be used to the low-density branches that form the “horseshoe” relation. HDBSCAN* and FLASC are also evaluated on the dataset as an example. All algorithms are manually tuned so their clusters best match the groups visible in a UMAP projection of the data.

%load_ext autoreload
%autoreload 2

import numpy as np
import pandas as pd

from umap import UMAP
from flasc import FLASC
from hdbscan import HDBSCAN
from biperscan import BPSCAN
from sklearn.preprocessing import StandardScaler

from lib.plotting import *
from matplotlib.colors import Normalize, to_rgb, ListedColormap
from matplotlib.lines import Line2D

tab10 = configure_matplotlib()

C:\Users\jelme\Documents\Development\work\flasc\pyflasc\src\flasc\plots.py:637: SyntaxWarning: invalid escape sequence '\l'
  axis.set_ylabel("$\lambda$ value")

First, we load the data and compute a UMAP embedding. UMAP is tuned to emphasize the data’s global structure. Specifically, we use a fairly high number of neighbours and low repulsion strength.

df = pd.read_csv("./data/diabetes/chemical_and_overt_diabetes.csv").iloc[:, 1:-1]
X = StandardScaler().fit_transform(df)

# X2 = UMAP(
#     n_neighbors=80, n_epochs=300, repulsion_strength=0.002, min_dist=0.1
# ).fit_transform(X)
# np.save("./data/diabetes/umap_embedding.npy", X2)

X2 = np.load("./data/diabetes/umap_embedding.npy")

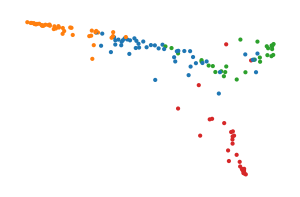
Now we plot the data colouring points by the area under their glucose curve in red and the area under their insulin area in blue. The peaks of both features correspond to the branches:

glucose_norm = Normalize(df[" glucose area"].min(), df[" glucose area"].max())
glucose_colors = [
    (*to_rgb(plt.cm.Reds(glucose_norm(x))), glucose_norm(x))
    for x in df[" glucose area"]
]
insulin_norm = Normalize(df[" insulin area"].min(), df[" insulin area"].max())
insulin_colors = [
    (*to_rgb(plt.cm.Blues(insulin_norm(x))), insulin_norm(x))
    for x in df[" insulin area"]
]

sized_fig(0.33)
plt.scatter(*X2.T, s=1, color="silver")
plt.scatter(*X2.T, s=1, c=glucose_colors)
plt.scatter(*X2.T, s=1, c=insulin_colors)
plt.legend(
    loc="lower left",
    handles=[
        Line2D([0], [0], linewidth=0, marker=".", color="r", label="AUCG"),
        Line2D([0], [0], linewidth=0, marker=".", color="b", label="AUCI"),
    ],
)
plt.axis("off")
plt.subplots_adjust(0, 0, 1, 1)
plt.savefig("images/diabetes_umap.pdf", pad_inches=0)
plt.show()

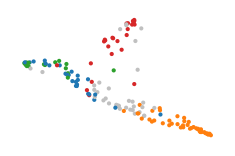
HDBSCAN struggles to detect these branches as distinct clusters. Only with the leaf cluster selection method and low min samples values will HDBSCAN detect small density peaks in the branches.

sized_fig(0.33)
c = HDBSCAN(min_cluster_size=5, cluster_selection_method="leaf").fit(X)
cmap = ListedColormap(["silver"] + [plt.cm.tab10.colors[i] for i in range(10)])
plt.scatter(*X2.T, c=c.labels_, s=1, cmap=cmap, vmin=-1, vmax=9)
plt.axis("off")
plt.subplots_adjust(0, 0, 1, 1)
plt.savefig("images/diabetes_hdbscan.pdf", pad_inches=0)
plt.show()

c:\Users\jelme\miniforge3\Lib\site-packages\sklearn\utils\deprecation.py:132: FutureWarning: 'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
  warnings.warn(
c:\Users\jelme\miniforge3\Lib\site-packages\sklearn\utils\deprecation.py:132: FutureWarning: 'force_all_finite' was renamed to 'ensure_all_finite' in 1.6 and will be removed in 1.8.
  warnings.warn(

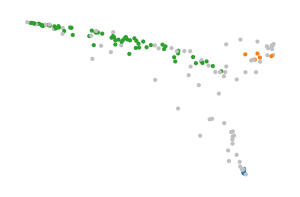
BPSCAN’s labels more closely match the projected shape (though, blue and red should be seen as a single cluster). The algorithm does require a carefully tuned min. samples value.

sized_fig(0.33)
c = BPSCAN(min_samples=5, min_cluster_size=15).fit(X)
plt.scatter(*X2.T, c=c.labels_, s=1, cmap=cmap, vmin=-1, vmax=9)
plt.axis("off")
plt.subplots_adjust(0, 0, 1, 1)
plt.savefig("images/diabetes_bpscan.pdf", pad_inches=0)
plt.show()

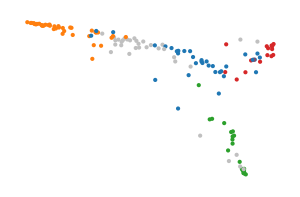
FLASC most accurately describes this dataset, as a single cluster with three branches. Most of the cluster is fairly central, indicated by the blue cluster. The other clusters indicate the branches, one of which is also very central and could be tuned out using a persistence threshold. FLASC also requires tuning, min. samples and min. branch size need to be set to low values to prevent cross-branch connectivity of the least central points.

sized_fig(0.33)
c2 = FLASC(
    min_samples=5,
    min_branch_size=25,
    allow_single_cluster=True,
    branch_detection_method="core",
).fit(X)
plt.scatter(*X2.T, c=c2.labels_, s=1, cmap=cmap, vmin=-1, vmax=9)
plt.axis("off")
plt.subplots_adjust(0, 0, 1, 1)
plt.savefig("images/diabetes_flasc.pdf", pad_inches=0)
plt.show()