Demo: Non-uniform Swiss roll

This notebook demonstrates how the noisy minimum spanning tree union (\(n\)-MST) and \(k\)-nearest minimum spanning tree (\(k\)-MST) behave on a Swiss roll with a sampling-gap. Our goal is to find a graph with a single connected component that describes the roll’s structure without shortcuts. This example demonstrates the methods’ ability to cross sampling gaps.

%load_ext autoreload
%autoreload 2

import numpy as np
import matplotlib.pyplot as plt
from umap import UMAP

from multi_mst import KMST, KMSTDescent, NoisyMST
from lib.drawing import draw_graph, draw_umap, draw_force

Swiss Roll

The spiral dataset contains a (roughly) uniformly-sampled 3D spiral with a sampling-gap:

# Load from ./data/generated/ instead if you want to update the spiral
D = np.load("./data/spiral/generated/X.npy")
LZ = np.load("./data/spiral/generated/lz.npy")
D.shape

(22196, 3)

The sampling gap was created by removing specific length–depth samples creating a ribbon-like point within the manifold:

plt.figure(figsize=(1.7438, 1.7438))
plt.scatter(LZ[:, 0], LZ[:, 1], edgecolors='none', linewidth=0, s=1, alpha=0.2)
plt.xlabel('spiral length')
plt.ylabel('depth')
plt.subplots_adjust(.23,.25)
plt.savefig('./images/spiral_gap_params.png', dpi=600, pad_inches=0)
plt.show()

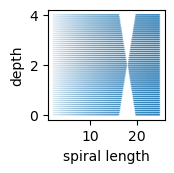
From the top-down, it looks like a sparse region / gap:

plt.figure(figsize=(1.7438, 1.7438))
plt.scatter(D[:, 0], D[:, 1], edgecolors='none', linewidth=0, s=1, alpha=0.2)
plt.gca().set_aspect('equal')
plt.axis('off')
plt.subplots_adjust(0, 0, 1, 1)
plt.savefig('./images/spiral_gap.png', dpi=600, pad_inches=0)
plt.show()

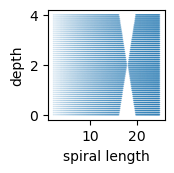
UMAP

UMAP is used to demonstrate \(k\)-nearest neighbour network approaches on this dataset. Notice how at low values of \(k\) many separate components are detected. At higher values of \(k\) a single component emerges, but shortcuts are also introduced.

def run_umap(k):
    p = UMAP(
        n_neighbors=k,
        init='random' if k == 2 else 'spectral',
    ).fit(D)
    draw_umap(p, color=LZ[:, 0], name='spiral_gap', alg=f'umap_{k}')
    draw_force(p, color=LZ[:, 0], name='spiral_gap', alg=f'umap_{k}')
    draw_graph(p, D[:, 0], D[:, 1], color=LZ[:, 0], name='spiral_gap', alg=f'umap_{k}')

run_umap(2)

%%timeit
p = UMAP(n_neighbors=2, transform_mode='graph').fit(D)

95 ms ± 1.55 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

run_umap(5)

%%timeit
p = UMAP(n_neighbors=5, transform_mode='graph').fit(D)

123 ms ± 2.15 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

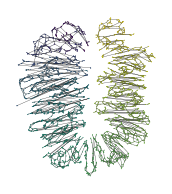
\(k\)-MST

The \(k\)-MST captures the global connectivity with few edges at low values of \(k\):

p = KMST(num_neighbors=2).fit(D).umap()
draw_umap(p, color=LZ[:, 0], name='spiral_gap', alg=f'kmst_2')
draw_force(p, color=LZ[:, 0], name='spiral_gap', alg=f'kmst_2')
draw_graph(p, D[:, 0], D[:, 1], color=LZ[:, 0], name='spiral_gap', alg=f'kmst_2')

%%timeit
p = KMST(num_neighbors=2).fit(D).umap(transform_mode='graph')

123 ms ± 2.66 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

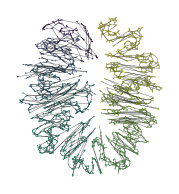
Approximate \(k\)-MST

An approximate \(k\)-MST version is quicker on datasets with many dimensions, not necessarily this dataset.

p = KMSTDescent(num_neighbors=2).fit(D).umap()
draw_umap(p, color=LZ[:, 0], name='spiral_gap', alg=f'kmst_descent_2')
draw_force(p, color=LZ[:, 0], name='spiral_gap', alg=f'kmst_descent_2')
draw_graph(p, D[:, 0], D[:, 1], color=LZ[:, 0], name='spiral_gap', alg=f'kmst_descent_2')

%%timeit
p = KMSTDescent(num_neighbors=2).fit(D).umap(transform_mode='graph')

1.1 s ± 94.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

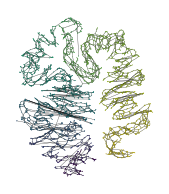
Noisy MST

The \(n\)-MST behaves similarly, but the noise can introduce shortcuts.

p = NoisyMST(num_trees=2, noise_fraction=0.6).fit(D).umap()
draw_umap(p, color=LZ[:, 0], name='spiral_gap', alg=f'nmst_2')
draw_force(p, color=LZ[:, 0], name='spiral_gap', alg=f'nmst_2')
draw_graph(p, D[:, 0], D[:, 1], color=LZ[:, 0], name='spiral_gap', alg=f'nmst_2')

%%timeit
p = NoisyMST(num_trees=2, noise_fraction=0.6).fit(D).umap(transform_mode='graph')

182 ms ± 2.45 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)