Example: Branches in 3D Horse

This notebook demonstrates how FLASC behaves on a 3D point cloud of a horse. This point cloud consists of 3D points sampled from the surface of a horse. The sampling density varies with the level of detail on the surface. For example, there are a lot more points on the head than on the stomach. In addition, the data-set has several hollow regions, which FLASC’s centrality metric has to deal with accurately.

The horse-shaped mesh-reconstructionn dataset is obtained from a STAD repository. The meshes were originally created or adapted for a paper by Robert W. Sumner and Jovan Popovic (2004). They can be downloaded and are described in more detail on their website.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from flasc import FLASC

from lib.plotting import *
palette = configure_matplotlib()

df = pd.read_csv('./data/horse/horse.csv')
X = df.to_numpy()

sized_fig(1, aspect=0.618/3)
plt.subplot(1, 3, 1)
plt.scatter(X.T[2], X.T[1], 1, alpha=0.1)
frame_off()
plt.subplot(1, 3, 2)
plt.scatter(X.T[2], X.T[0], 1, alpha=0.1)
frame_off()
plt.subplot(1, 3, 3)
plt.scatter(X.T[0], X.T[1], 1, alpha=0.1)
frame_off()
plt.show()

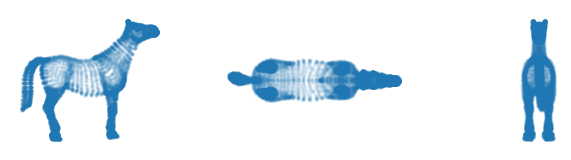
Single cluster

First, lets analyze this dataset as if it is a single cluster. For that purpose, we set override_cluster_labels to assign every point to the 0 cluster. This is different from allow_single_cluster, as it gives each point the same cluster membership probability. All branches in this point cloud (legs, head, and tail) are quite large, so we set min_branch_size=20. Because there are no noise points and to speed up the result, we keep min_samples=5. Note that this value is unlikely to cross the hollow regions in the legs and torso.

c = FLASC(min_samples=5, min_branch_size=20, branch_selection_method="leaf").fit(
    X, labels=np.zeros(X.shape[0], dtype=np.intp)
)
g = c.cluster_approximation_graph_

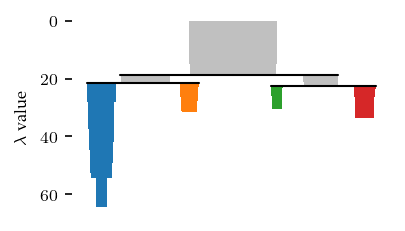
With these settings, we find 2 main sides of the cluster, with 3 persistent branches each.

sized_fig()
c.branch_condensed_trees_[0].plot(leaf_separation=0.2)
plt.ylabel('Eccentricity')
plt.show()

The resulting branches neatly correspond to the legs, head, ears and tail. The torso gets its own label, indicating the most central points.

sized_fig(1, aspect=0.618/3)
plt.subplot(1, 3, 1)
plt.scatter(X.T[2], X.T[1], 1, c.labels_,
            alpha=0.1, cmap='tab10', vmax=10)
frame_off()
plt.subplot(1, 3, 2)
plt.scatter(X.T[2], X.T[0], 1, c.labels_,
            alpha=0.1, cmap='tab10', vmax=10)
frame_off()
plt.subplot(1, 3, 3)
plt.scatter(X.T[0], X.T[1], 1, c.labels_,
            alpha=0.1, cmap='tab10', vmax=10)
frame_off()
plt.show()

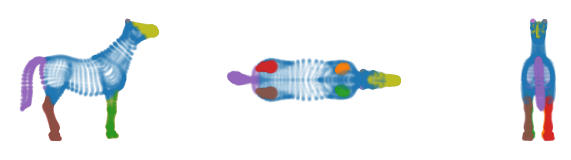
Computing the branch membership vectors to re-assign central points to the closest branch centroid in the cluster approximation graph lets each branch grow into the torso for a potentially more useful segmentation.

from flasc.prediction import (
    branch_centrality_vectors,
    update_labels_with_branch_centrality,
)

v = branch_centrality_vectors(c)
l, _ = update_labels_with_branch_centrality(c, v)

sized_fig(1, aspect=0.618 / 3)
plt.subplot(1, 3, 1)
plt.scatter(X.T[2], X.T[1], 1, l, alpha=0.1, cmap="tab10", vmax=10)
frame_off()
plt.subplot(1, 3, 2)
plt.scatter(X.T[2], X.T[0], 1, l, alpha=0.1, cmap="tab10", vmax=10)
frame_off()
plt.subplot(1, 3, 3)
plt.scatter(X.T[0], X.T[1], 1, l, alpha=0.1, cmap="tab10", vmax=10)
frame_off()
plt.show()

Multiple clusters

This data set can also be viewed as multiple density-based clusters. To cluster this dataset we specify min_samples=20 and min_cluster_size=1000. This results in four clusters: the tail, the head, the back legs, and the front legs. Parts of the torse are classified as noise. To detect branches within these clusters, we set min_branch_size=20 and branch_selection_persistence=0.1.

c = FLASC(
    min_samples=20,
    min_cluster_size=1000,
    min_branch_size=20,
    branch_selection_persistence=0.1,
).fit(X)
g = c.cluster_approximation_graph_

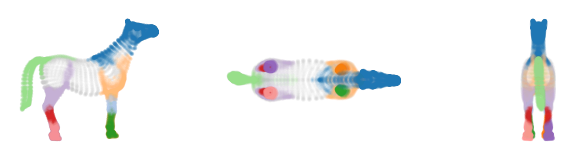
The clustering found 2 sides the each contain 2 clusters.

sized_fig()
c.condensed_tree_.plot()
plt.show()

The resulting clusters neatly capture the tail, back legs, front legs and head.

sized_fig(1, aspect=0.618/3)
plt.subplot(1, 3, 1)
colors = [palette[l]  if l >= 0 else (0.8, 0.8, 0.8) for l in c.cluster_labels_]
plt.scatter(X.T[2], X.T[1], 1, colors,
            alpha=0.1)
frame_off()
plt.subplot(1, 3, 2)
plt.scatter(X.T[2], X.T[0], 1, colors,
            alpha=0.1)
frame_off()
plt.subplot(1, 3, 3)
plt.scatter(X.T[0], X.T[1], 1, colors,
            alpha=0.1)
frame_off()
plt.show()

The branches detect the individual lower-legs, hips and shoulder-region as distinct branches.

sized_fig(1, aspect=0.618/3)
palette = plt.get_cmap('tab20').colors
plt.subplot(1, 3, 1)
colors = [
    palette[l]  if l >= 0 else (0.8, 0.8, 0.8)
    for l in c.labels_
]
plt.scatter(X.T[2], X.T[1], 1, colors,
            alpha=0.1)
frame_off()
plt.subplot(1, 3, 2)
plt.scatter(X.T[2], X.T[0], 1, colors,
            alpha=0.1)
frame_off()
plt.subplot(1, 3, 3)
plt.scatter(X.T[0], X.T[1], 1, colors,
            alpha=0.1)
frame_off()
plt.show()

The branch grouping is easier to see when drawn over the cluster approximation graphs. A potential issue with this segmentation is that the label for the most central points in the front-legs consists of two distinct connected component. This happens for U-shaped clusters in general, where the centroid lies between the branches, and both branches have a local centrality maximum.

sized_fig(1, aspect=1)
g.plot(edge_alpha=0.1, node_color=[
    palette[l % 20] for l in c.labels_[g.point_mask]
])
frame_off()
plt.show()

C:\Users\jelme\Documents\Development\work\clones\hdbscan\hdbscan\plots.py:1179: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
  plt.scatter(

These graphs also show how the centrality metric behaves.

sized_fig(1, aspect=1)
g.plot(node_alpha=0, edge_color='centrality', edge_alpha=0.1)
frame_off()
plt.show()